[코테] 리트코드 배열 42. Trapping Rain Water

42. Trapping Rain Water

문제 링크

https://leetcode.com/problems/trapping-rain-water/description/

문제 설명

Given n non-negative integers representing an elevation map where the width of each bar is 1, compute how much water it can trap after raining.

제한 사항

• n == height.length
• 1 <= n <= 2 * 104
• 0 <= height[i] <= 105

입출력 예 #1

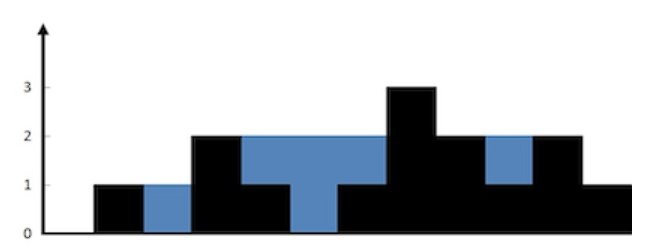
1. Input: height = [0,1,0,2,1,0,1,3,2,1,2,1]
2. Output: 6
3. Explanation: The above elevation map (black section) is represented by array [0,1,0,2,1,0,1,3,2,1,2,1]. In this case, 6 units of rain water (blue section) are being trapped.

입출력 예 #2

1. Input: height = [4,2,0,3,2,5]
2. Output: 9

문제 풀이

투포인터 기법 또는 스택 쌓기로 문제 풀이 가능하다.

아직 나한테는 어려운 거 보니 갈 길이 멀다.

## 투 포인터를 최대로 이동
class Solution:
    def trap(self, height: List[int]) -> int:
        if not height :
            return 0
        
        volume = 0
        left, right = 0, len(height) - 1
        left_max, right_max = height[left], height[right]

        while left < right :
            left_max, right_max = max(height[left], left_max), max(height[right], right_max)
            
            # 더 높은 쪽을 향해 투 포인터 이동
            if left_max <= right_max : 
                volume += left_max - height[left]
                left += 1
            else : 
                volume += right_max - height[right]
                right -= 1
        
        return volume

## 스택 쌓기
class Solution:
    def trap(self, height: List[int]) -> int:
        stack = []
        volume = 0

        for i in range(len(height)):
            # 변곡점을 만나는 경우
            while stack and height[i] > height[stack[-1]]:
                # 스택에서 꺼낸다.
                top = stack.pop()

                if not len(stack):
                    break
                
                # 이전과의 차이만큼 물 높이 처리
                distance = i - stack[-1] -1
                waters = min(height[i], height[stack[-1]]) - height[top]

                volume += distance * waters

            stack.append(i)
            
        return volume