[코테] 리트코드 최단 경로 787. Cheapest Flights Within K Stops

787. Cheapest Flights Within K Stops

문제 링크

https://leetcode.com/problems/cheapest-flights-within-k-stops/description/

문제 설명

There are n cities connected by some number of flights. You are given an array flights where flights[i] = [fromi, toi, pricei] indicates that there is a flight from city fromi to city toi with cost pricei.

You are also given three integers src, dst, and k, return the cheapest price from src to dst with at most k stops. If there is no such route, return -1.

제한 사항

• 1 <= n <= 100
• 0 <= flights.length <= (n * (n - 1) / 2)
• flights[i].length == 3
• 0 <= fromi, toi < n
• fromi != toi
• 1 <= pricei <= 104
• There will not be any multiple flights between two cities.
• 0 <= src, dst, k < n
• src != dst

입출력 예 #1

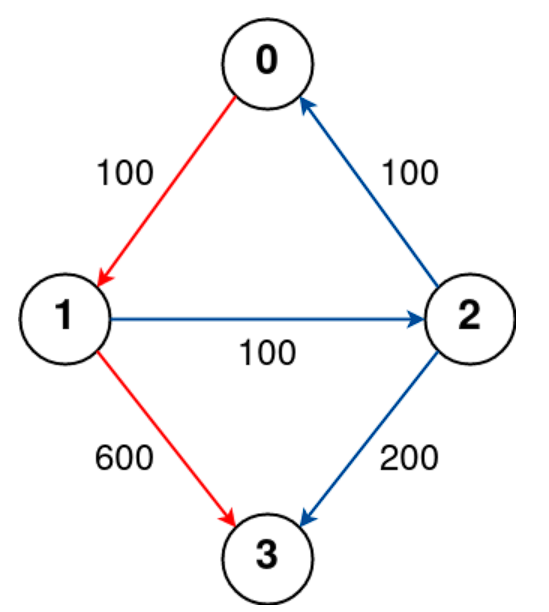
1. Input : n = 4, flights = [[0,1,100],[1,2,100],[2,0,100],[1,3,600],[2,3,200]], src = 0, dst = 3, k = 1
2. Output : 700
3. Explanation : The graph is shown above. The optimal path with at most 1 stop from city 0 to 3 is marked in red and has cost 100 + 600 = 700. Note that the path through cities [0,1,2,3] is cheaper but is invalid because it uses 2 stops.

입출력 예 #2

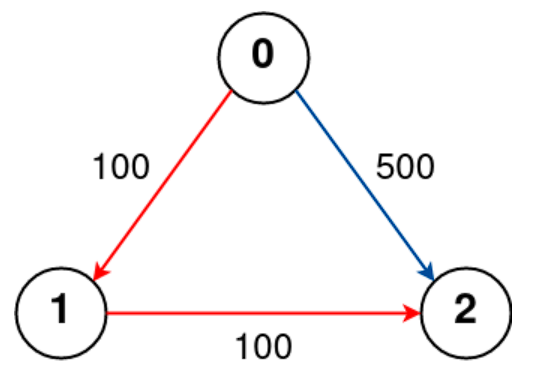
1. Input : n = 3, flights = [[0,1,100],[1,2,100],[0,2,500]], src = 0, dst = 2, k = 1
2. Output : 200
3. Explanation : The graph is shown above. The optimal path with at most 1 stop from city 0 to 2 is marked in red and has cost 100 + 100 = 200.

입출력 예 #3

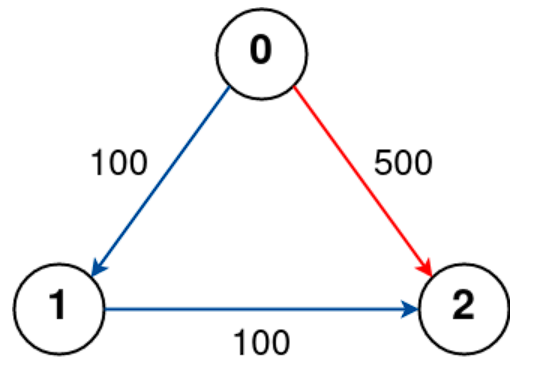
1. Input : n = 3, flights = [[0,1,100],[1,2,100],[0,2,500]], src = 0, dst = 2, k = 0
2. Output : 500
3. Explanation : The graph is shown above. The optimal path with no stops from city 0 to 2 is marked in red and has cost 500.

문제 풀이

bfs 기법 및 우선순위 큐 기법을 이용하여 문제를 풀면 된다.

하지만 책에 있는 풀이를 그대로 사용할 경우 시간초과가 걸려 해결할 수 없다.

거기서 추가적으로 이미 방문한 노드는 방문하지 않도록 비교하는 구문까지 추가한다.

class Solution:
    def findCheapestPrice(self, n: int, flights: List[List[int]], src: int, dst: int, K: int) -> int:
        graph = collections.defaultdict(list)
        # 그래프 인접 리스트 구성
        for u, v, w in flights:
            graph[u].append((v, w))
        
        # 큐 변수: [(가격, 정점, 경유지 수)]
        Q = [(0, src, 0)]
        visit = {}

        # 우선순위 큐 최솟값 기준으로 도착점까지 최소 비용 판별
        while Q:
            price, node, k = heapq.heappop(Q)
            if node == dst:
                return price
            if node not in visit or visit[node] > k:
                visit[node] = k
                for v, w in graph[node]:
                    if k <= K:
                        alt = price + w
                        heapq.heappush(Q, (alt, v, k + 1))
        return -1