[코테] 리트코드 트리 310. Minimum Height Trees

310. Minimum Height Trees

문제 링크

https://leetcode.com/problems/minimum-height-trees/description/

문제 설명

A tree is an undirected graph in which any two vertices are connected by exactly one path. In other words, any connected graph without simple cycles is a tree.

Given a tree of n nodes labelled from 0 to n - 1, and an array of n - 1 edges where edges[i] = [ai, bi] indicates that there is an undirected edge between the two nodes ai and bi in the tree, you can choose any node of the tree as the root. When you select a node x as the root, the result tree has height h. Among all possible rooted trees, those with minimum height (i.e. min(h)) are called minimum height trees (MHTs).

Return a list of all MHTs’ root labels. You can return the answer in any order.

The height of a rooted tree is the number of edges on the longest downward path between the root and a leaf.

제한 사항

• 1 <= n <= 2 * 10^4
• edges.length == n - 1
• 0 <= ai, bi < n
• ai != bi
• All the pairs (ai, bi) are distinct.
• The given input is guaranteed to be a tree and there will be no repeated edges.

입출력 예 #1

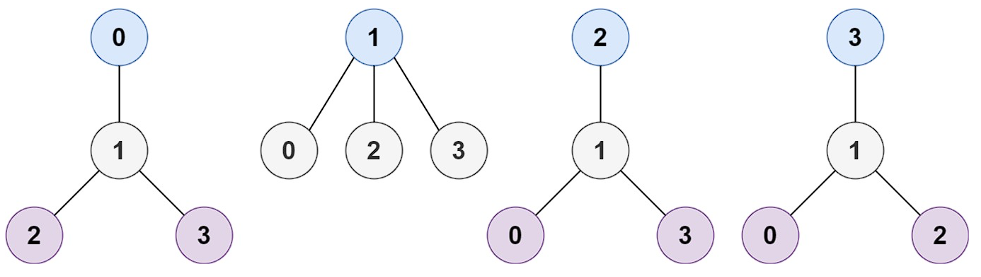
1. Input : n = 4, edges = [[1,0],[1,2],[1,3]]
2. Output : [1]
3. Explanation : As shown, the height of the tree is 1 when the root is the node with label 1 which is the only MHT.

입출력 예 #2

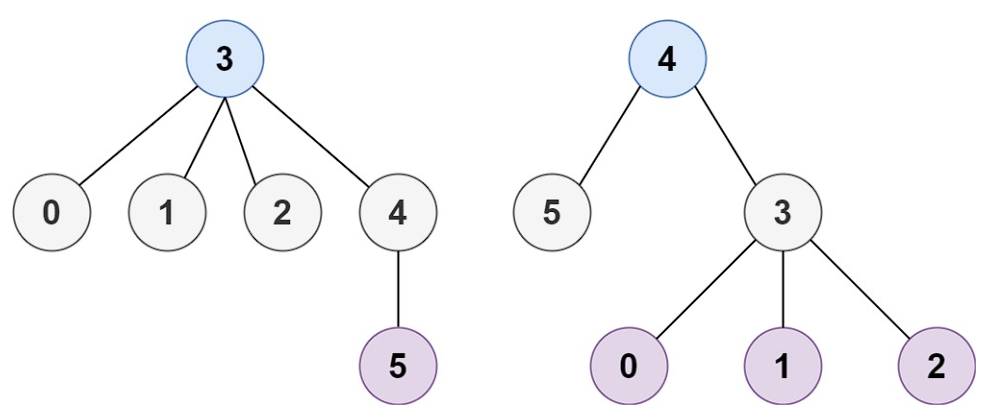
1. Input : n = 6, edges = [[3,0],[3,1],[3,2],[3,4],[5,4]]
2. Output : [3,4]

문제 풀이

재귀를 이용하여 왼쪽 노드와 오른쪽 노드의 높이차를 구하여 균형 이진 탐색 트리인지 확인한다.

class Solution:
    def findMinHeightTrees(self, n: int, edges: List[List[int]]) -> List[int]:
        if n <= 1:
            return [0]

        # 양방향 그래프 구성
        graph = collections.defaultdict(list)
        for i, j in edges:
            graph[i].append(j)
            graph[j].append(i)

        # 첫 번째 리프 노드 추가
        leaves = []
        for i in range(n + 1):
            if len(graph[i]) == 1:
                leaves.append(i)
            
        # 루트 노드만 남을 때까지 반복 제거
        while n > 2:
            n -= len(leaves)
            new_leaves = []
            for leaf in leaves:
                neighbor = graph[leaf].pop()
                graph[neighbor].remove(leaf)

                if len(graph[neighbor]) == 1:
                    new_leaves.append(neighbor)
        
            leaves = new_leaves

        return leaves