[코테] 백준 브루트포스 1248번 문제

1248번 : Guess

문제 링크

https://www.acmicpc.net/problem/1248

문제 설명

Given a sequence of integers, a1, a2, …, an, we define its sign matrix S such that, for 1 ≤ i ≤ j ≤ n, Sij=”+” if ai + … + aj > 0; Sij=”−” if ai + … + aj < 0; and Sij=”0” otherwise.

For example, if (a1, a2, a3, a4)=( −1, 5, −4, 2), then its sign matrix S is a 4×4 matrix:

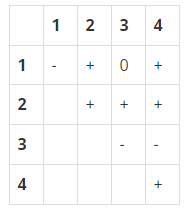
We say that the sequence (−1, 5, −4, 2) generates the sign matrix. A sign matrix is valid if it can be generated by a sequence of integers.

Given a sequence of integers, it is easy to compute its sign matrix. This problem is about the opposite direction: Given a valid sign matrix, find a sequence of integers that generates the sign matrix. Note that two or more different sequences of integers can generate the same sign matrix. For example, the sequence (−2, 5, −3, 1) generates the same sign matrix as the sequence (−1,5, −4,2).

Write a program that, given a valid sign matrix, can find a sequence of integers that generates the sign matrix. You may assume that every integer in a sequence is between −10 and 10, both inclusive.

입력

The first line contains an integer n(1 ≤ n ≤ 10), where n is the length of a sequence of integers. The second line contains a string of n(n+1)/2 characters such that the first n characters correspond to the first row of the sign matrix, the next n−1 characters to the second row, …, and the last character to the n-th row.

출력

Output exactly one line containing a sequence of n integers which generates the sign matrix. If more than one sequence generates the sign matrix, you may output any one of them. Every integer in the sequence must be between −10 and 10, both inclusive.

문제풀이

1. 입력받은 부호들을 배열 형태로 저장한다.
2. -10부터 10끼지 수를 순회하면고 해당 수가 부호배열의 조건에 맞는지를 검사
3. 조건 검사 : 만약 dp배열에 저장될 3번째 수를 검사하고자 한다면 1~3번째 수의 합 / 2~3번째 수의 합 / 3번째 수의 부호가 각각 조건과 맞는지 확인
4. dp배열의 크기가 N과 일치하면 result 결과에 저장하고, 현재 돌고 있는 재귀문들을 모두 종료 (pypy3로 해야 통과)

N = int(input())
arr = [['0' for _ in range(N)] for _ in range(N)]
signs = list(input())

# 부호 배열 저장
idx = 0 
for i in range(N) : 
    for j in range(i, N) : 
        arr[i][j] = signs[idx]
        idx += 1

# dp : 임시 배열 / result : 결과 배열
dp = []
result = ''
def back() : 
    global result
    
    if len(dp) == N :    # dp배열의 크기가 N과 같으면 result배열에 결과 저장
        result = " ".join(list(map(str, dp)))
        return

    if result != '' :    # result배열에 이미 값이 들어와 있다면 재귀문들을 모두 종료
        return
        
    for i in range(-10, 11) :    # -10~10까지의 수를 순회
        
        if len(dp) == 0 :    # dp배열에 아무것도 없다면 아래 조건 수행
            if (arr[0][0] == '-' and i < 0) or     # 해당 수가 부호에 맞는지 확인
               (arr[0][0] == '0' and i == 0) or 
               (arr[0][0] == '+' and i > 0):
                dp.append(i)
                back()
                dp.pop()
            else :
                continue

        else :    # dp배열에 1개 이상 항목이 있을 때 아래 조건 수행
            for j in range(len(dp)+1) :    # 해당 수가 부호배열의 조건에 맞는지 검사
                if arr[j][len(dp)] == '-' and sum(dp[j:len(dp)]) + i >= 0 :
                    break
                if arr[j][len(dp)] == '0' and sum(dp[j:len(dp)]) + i != 0 :
                    break
                if arr[j][len(dp)] == '+' and sum(dp[j:len(dp)]) + i <= 0 :
                    break
            else :    # 검사들을 모두 통과 시 재귀 진행
                dp.append(i)
                back()
                dp.pop()  
back()
print(result)