[코테] 프로그래머스 동적계획법 사칙 연산

사칙연산

문제 링크

https://school.programmers.co.kr/learn/courses/30/lessons/1843

문제 설명

사칙연산에서 더하기(+)는 결합법칙이 성립하지만, 빼기(-)는 결합법칙이 성립하지 않습니다.

예를 들어 식 1 - 5 - 3은 연산 순서에 따라 다음과 같이 다른 결과를 가집니다.

• ((1 - 5) - 3) = -7
• (1 - (5 - 3)) = -1

위 예시와 같이 뺄셈은 연산 순서에 따라 그 결과가 바뀔 수 있습니다. 또 다른 예로 식 1 - 3 + 5 - 8은 연산 순서에 따라 다음과 같이 5가지 결과가 나옵니다.

• (((1 - 3) + 5) - 8) = -5
• ((1 - (3 + 5)) - 8) = -15
• (1 - ((3 + 5) - 8)) = 1
• (1 - (3 + (5 - 8))) = 1
• ((1 - 3) + (5 - 8)) = -5

위와 같이 서로 다른 연산 순서의 계산 결과는 [-15, -5, -5, 1, 1]이 되며, 이중 최댓값은 1입니다. 문자열 형태의 숫자와, 더하기 기호(“+”), 뺄셈 기호(“-“)가 들어있는 배열 arr가 매개변수로 주어질 때, 서로 다른 연산순서의 계산 결과 중 최댓값을 return 하도록 solution 함수를 완성해 주세요.

제한 사항

• arr는 두 연산자 “+”, “-“ 와 숫자가 들어있는 배열이며, 길이는 3 이상 201 이하 입니다.
• arr의 길이는 항상 홀수입니다.
• arr에 들어있는 숫자의 개수는 2개 이상 101개 이하이며, 연산자의 개수는 (숫자의 개수) -1 입니다.
• 숫자는 1 이상 1,000 이하의 자연수가 문자열 형태로 들어있습니다.. (ex : “456”)
• 배열의 첫 번째 원소와 마지막 원소는 반드시 숫자이며, 숫자와 연산자가 항상 번갈아가며 들어있습니다.

입출력 예

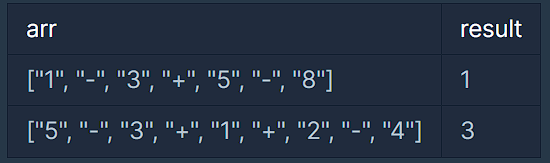
입출력 예시

입출력 예 #1

위의 예시와 같이 (1-(3+(5-8))) = 1 입니다.

입출력 예 #2

(5-(3+((1+2)-4))) = 3 입니다.

문제 풀이

자세한 내용은 아래 블로그 참고

https://school.programmers.co.kr/questions/64429

1. 더하기는 괄호를 씌울 필요가 없고, 빼기만 신경써서 괄호를 만들면 된다.
2. 배열에서 빼기 기호를 기준으로 지역을 나눈다.
3. 들어가는 숫자는 모두 양수이기에 빼기에 괄호를 씌울때 최댓값은 맨 앞에만 씌운 값, 최솟값은 괄호를 전체를 씌운 값이 된다.
4. 따라서 배열을 뒤에서부터 앞으로 순회하면서 최댓값은 (현재 윈도우의 최댓값 + 뒤 지역의 최댓값) 또는 (현재 윈도우의 최솟값 - 뒤 지역의 최솟값) (현재 윈도우를 최소로 하더라도 뒤 지역의 부호를 변경하고자 함)

def solution(arr):
    arr = ''.join(arr).split('-')
    answer = sum([*map(int, arr[0].split('+'))])

    min_tail, max_tail = 0, 0
    for a in arr[:0:-1] :
        nums = [*map(int, a.split('+'))]
        min_sub = -sum(nums)
        max_sub = -2 * nums[0] - min_sub
        max_tail, min_tail = max(max_sub + max_tail, min_sub - min_tail), min(min_sub + min_tail, min_sub - max_tail)
        
    return answer + max_tail

arr = ["5", "-", "3", "+", "1", "+", "2", "-", "4"]
solution(arr)